What is the start angle of an elliptic arc?

One of the properties of circular and elliptical arcs is the "start angle". When I draw a circular arc the meaning of it's start angle is quiet obvious. The start angle of the following arc is 45°:


However for an elliptic arc it is not clear to me what the meaning of a 45° "start angle" would be. The following elliptical arc has a start angle of 45° (set by me in the properties), but what does this start angle mean?

Maybe the naming "start angle" and "end angle" is not optimal.
In DXF reference these values are named "parameter" instead of "angle".

Basically these values are angles, the range is from 0 to 2*PI, respective 0° to 360°.
The formula how start/end points are calculated, is explained in DXF reference too.
For details see https://www.autodesk.com/techpubs/autocad/acad2000/dxf/ellipse_command39s_parameter_option_dxf_06.htm

Therefor the angles match with the circular arc in the X/Y axes (0°, 90°, 180°, 270°), because in these corner cases one of the operands (sin(0°/180°), cos(90°/270°)) becomes 0.

A less mathematical explanation is this:

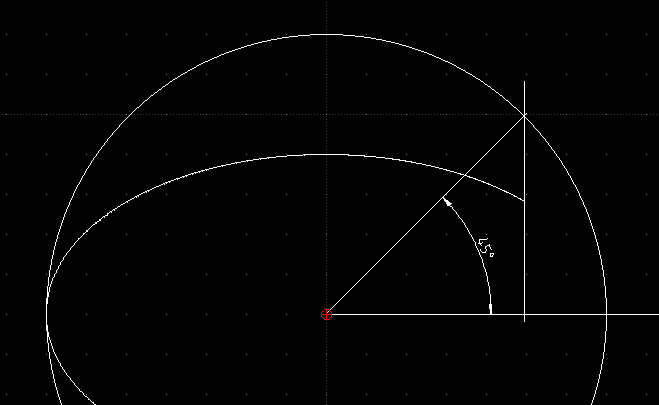
An ellipse is a distorted circle.
Draw a circle in the center of the ellipse with the radius of major axis.
Then construct the intersection of a 45° center ray with the circles circumference and draw a line parallel to the Y axis through the intersection point.
Where the vertical line intersects the ellipse is the calculated start/end point.

Armin

Thanks, Praise the LordOfBikes!
pwp