Isometric Circles
|
Hi,
Not only am I a LibreCAD newbie, I'm a CAD newbie, so please treat me gently. I've drawn up a bracket in isometric, but it has holes in it: or, actually, it should: I can't work out how to draw isometric circles. I've tried ellipses and splines, but I simply can't work out how to make that work properly. It seems such a simple task (and probably is), so could someone tell me what I should be doing? Thank you. |
|
1. Set the grid to isometric.
2. Set snap on grid (and deselect any other snap modes) 3. Draw 4 lines to form an isometric view square. 4. Select the "Draw Ellipse Inscribed in a Quadrilateral" tool and click on the 4 lines you have just drawn. Mike |
|
Mike, thank you for this.
I followed steps 1 - 3 rigorously, selected the "Draw Ellipse Inscribed in a Quadrilateral" tool but could only select 3 lines, not the fourth. Am I missing something? An ellipse appears after clicking on the third line, and the command line shows "Specify the fourth line" but it won't select. |
|
the feature "Draw Ellipse Inscribed in a Quadrilateral" only works when there's a unique inscribed ellipse.
Therefore, it doesn't work for: 1, trapezoid, there's no solution in general; 2, rectangle, there are infinite number of solutions; for case 2, we should implement a way to select a solution though.
|
|
In reply to this post by earthcaretech
Hi,
I didn't read carefully enough. it's about circles in isometric. You can use ellipse ( Center and two points, the first method in Draw -> Ellipse) together with command line (calculator) to get inscribed ellipse. The basic idea is that: the projection to isometric does not change scale ratios in the same direction ( say, along a line before and after projection). I will guide you through an example: 0, Edit -> Current Drawing Preferences-> Grid : choose isometric 1, start a new drawing; 2, snap to grid only in the snap toolbar, no restriction 3, Draw->line -> two points; 4, use command line (Ctl-M to activate or just click on the command line) to draw a square contour (square in 3D), i.e. a rhombus. (0, 0) , (200/sqrt(3), -50), (400/sqrt(3), 0) , (200/sqrt(3), 50). or (0, 0), (100, 0), (100, 100), (0, 100) in 3D; 4, Draw -> Ellipse -> Center and two points ; 5, use command for center: ( 200/sqrt(3), 0), i.e., the rhombus center; 6, set the end of major axis: which is 1/sqrt(2) to the rhombus vertex (400/sqrt(3), 0) which is relative to ellipse center ( 200/sqrt(3), 0). therefore, in command type in relative coordinates: @200/sqrt(3)/sqrt(2), 0 7, type in coordinates for the end of minor axis: again , 1/sqrt(2) factor relative to vertex ( 200/sqrt(3), -50). type in relative coordinates to ellipse center: @0, 50/sqrt(2) Since the ellipse orientation and its major/minor radii are just 1/sqrt(2) of known values, the construction it quite straight forward. isometric_circle.dxf 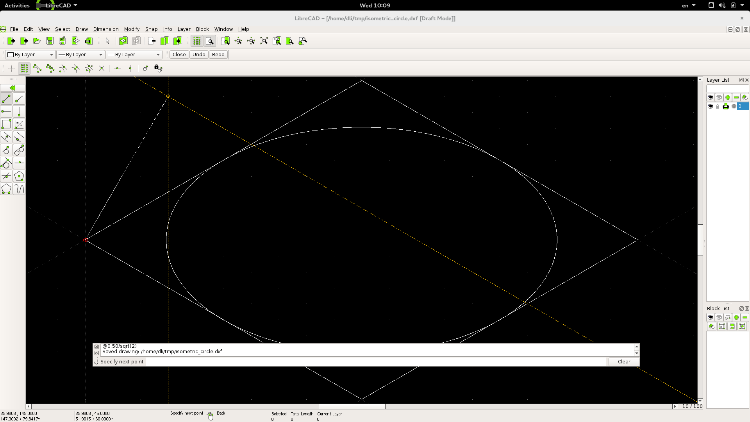
|
|
An isometric "square" is a four sided quadrilateral. All four sides are of equal length and each opposite pair of sides is parallel. So there should be a unique mathematical solution to an ellipse touching the midpoint of all four sides.
I've gone back and experimented with the method in my original post and it seems the "Draw Ellipse Inscribed in a Quadrilateral" tool is sensitive to the order in which the four lines are selected and or the direction they are drawn in (i.e. left to right, top to bottom, etc). For example, draw a rectangle using the "Rectangle" tool on a grid set to orthoganal. Then use the "Draw Ellipse Inscribed in a Quadrilateral" tool. If the sides are selected in the order left, bottom, top, right then the tool successfully draws an ellipse. But if the sides are selected in the order bottom, right, top, left then it doesn't work. The "Rectangle" tool always draws the lines in a specific order with a specific direction so the behaviour described above is at least predictable. But now try creating a rectangle by drawing four separate lines with the "Line" tool in random order and with random up/down left/right direction. Then use the "Draw Ellipse Inscribed in a Quadrilateral" tool and you will find that sometimes it works and sometimes it doesn't with no obvious pattern. Mike |
|
The general picture for inscribed ellipses of quadrilateral:
The is none, for a general trapezoid; There are infinite possibilities for a rectangle/rhombus We can add one more step in the drawing action, say, to specify a tangential point for rectangle/rhombus. Since rectangle/rhombus are probably most used cases, adding this feature makes sense.
|
|
I understand that what you are saying about the possible solutions to an ellipse inscribed in a quadilateral is correct in terms of pure mathematics.
However, the point is that the "Draw Ellipse Inscribed in a Quadrilateral" tool already does work with a rectangle. The only problem with the tool is that it seems to want the four sides to be selected in a paricular sequence as described in my previous post. So I'm guessing the code behind the tool is already doing something extra to create a unique solution. Perhaps it is making the ellipse touch the midpoints of the four selected lines? Mike |
|
Yes, you are correct.
The previous algorithm does not try to work out a general solution, but chooses the middle points as tangential points to define the inscribed. We can make this behavior robust, and user can choose to accept this ellipse or specify a tangential point.
|
|
I'm thoroughly confused: just how does the solution of drawing a rectangle in orthogonal mode help with an isometric circle? And I simply couldn't get the command line solution to work at all - although that's maybe because I'm a CAD and LibreCad newbie.
|
|
In reply to this post by Mike Hayes
The area of the inscribed ellipse (and other objects) should be the maximum. For this there is only one solution. I believe that this is a solution for isometric circles too. Midpoint is not good idea. Example:  |
|
Identified two bugs:
1 get line intersection tolerance issue 2 get eigen vectors for quadratic failed(rectangular case) This symmetric trapezoid needs new implementation, I will investigate
|
|
by this commit:
https://github.com/LibreCAD/LibreCAD/commit/b3f5959d9328c2f9fb41154a63630582499e2902 first two bugs are fixed. Still need to fix the symmetric trapezoid case. After that, we can think about handling infinite possible solutions.
|
|
In reply to this post by stranger573
Interesting enough.
To find the inscribed ellipse of a symmetric trapezoid can be converted to find roots of a quartic equation. The general algorithm by projection of inscribed circle of square doesn't apply here. There's no solution for asymmetric trapezoid.
|
|
This is all very interesting (to
someone, I suppose), but I'm no closer to solving my problem.
On 14/03/15 07:07, dxli [via LibreCAD]
wrote:
Interesting enough. --
Regards, EarthCare Technology (a division of Ironstone Technology Pty
Ltd) EarthCare Technology: Technology for a
sustainable world. http://www.earthcaretech.com.au -- This email is intended for the named addressee/s only and may
contain confidential or privileged information.
|
|
Edwin
The answer to what inscribing an ellipse inside a rectangle has to do with your original question, is just that it's the simplest case that the "Draw Ellipse Inscribed in a Quadrilateral" tool should be able to deal with. As you can see from the other posts in this thread, dxli has fixed the issues with the simple use of this tool and is now looking at more advanced mathematical cases. dxli's revisions won't be available until the next release of LibreCAD. So to solve your immediate problem I attach a DXF file IsometricCircles.dxf containing a left, right, and top view of an isometric circle of diameter 1 unit. To get them into your own drawing, use file>import>block from the menu. Once imported, explode the block, then copy the circles to wherever you like in your drawing and scale them to whatever size you require. Mike |
|
Thanks a lot! Mike.
On top of this, I recommend interested users to build LibreCAD from source. It helps the development side by providing fast feedbacks.
|
|
In reply to this post by Mike Hayes
Mike
Thank you for the file, which will help me out of my current issue. I knew something was going on that would ultimately be useful to someone; it just wasn't solving my immediate problem. But if my innocent question has led to a new feature of sorts, I'm glad - that's what open source is about. On 14/03/15 09:04, Mike Hayes [via
LibreCAD] wrote:
Edwin --
Regards, EarthCare Technology (a division of Ironstone Technology Pty
Ltd) EarthCare Technology: Technology for a
sustainable world. http://www.earthcaretech.com.au -- This email is intended for the named addressee/s only and may
contain confidential or privileged information.
|
|
In reply to this post by stranger573
implemented the case of symmetric trapezoid:
https://github.com/LibreCAD/LibreCAD/commit/a40e67708d3415b0b667dbbc2eb27a6b49313898 ellipse4.dxf 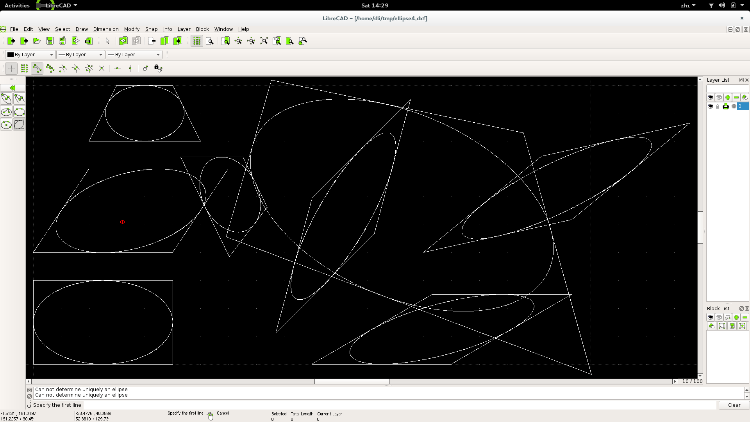
|
|
This makes the tool better and more useful. Thanks.
|
| Free forum by Nabble | Edit this page |




